Seite 4 von 7
Re: Existenz größter und kleinster Zahlen
Verfasst: Sonntag 13. September 2009, 16:20
von Todoroff
Trockennasenaffe RPL32P12
Das heißt Peano und nicht Paeno. Wie lauten die?
Wir diskutieren hier über eine Erweiterung der Mathematik. Sie müssen das doch nicht mitmachen.
Wie die lauten hat LaughingMan in diesem Thema geschrieben.
Noch nicht bemerkt, daß 1-0,999... Teil der Menge der reellen Zahlen ist und die Peano-Axiome nur natürliche Zahlen betreffen? Was Schwatzen Sie für einen unglaublichen Unfug daher? Begeben Sie sich in Behandlung.
"Hallo, können sie mir sagen, wo die andere Straßenseite ist?"
"Ja, da drüben!"
"Komisch, die schicken mich immer hier rüber!"
Ihr Niveau.
Re: Existenz größter und kleinster Zahlen
Verfasst: Sonntag 13. September 2009, 16:30
von Todoroff
Trockennasenaffe RPL32P12
Hiermit erkläre ich Sie zum DAU, zum Dümmsten Anzunehmenden User dieses Forums.
*)
Bernoullische Ungleichung
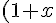^n\ge~(1+nx))
ist nicht anzuwenden auf (wie Sie das fälschlicherweise tun, weshalb Ihr Beweis nichts wert ist:
\left(1-\frac{1}{n^2}\right)^{n-1}\ge^*\left(1+\frac{1}{n}\right)\left(1-(n-1)\frac{1}{n^2}\right)=1+\frac{1}{n^3}\ge~1)
Das ist nicht anzuwenden?
Korrekt
Wikipedia - Bernoullische Ungleichung hat geschrieben:Für jede reelle Zahl

und jede nicht negative ganze Zahl

gilt
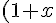^n\ge~1+nx)
.
Wir haben hier
^{n-1})
für eine natürliche Zahl n, mit n > 1.
Ist

eine reelle Zahl größer oder gleich -1? Ja, ist sie.
Ist der Exponent n-1 eine ganze Zahl, größer oder gleich 0? Ja, ist sie.
Demnach ist die Bernoullische Ungleichung hier anwendbar und es folgt:
Sie ist nicht anzuwenden, da es eine Summe voraussetzt und Sie es für eine Differenz anwenden.
q.e.d.
Ich wußte, daß Sie so unglaublich bescheuert sind, und das selbst dann nicht bemerken, wenn man es Ihnen aufs Brot schmiert. Absolut eines DAU's würdig.
Alte Lumpen reingewaschen
helfen manchem aus den Aschen.
Re: Existenz größter und kleinster Zahlen
Verfasst: Sonntag 13. September 2009, 20:03
von Todoroff
Trockennasenaffe RPL32P12
... das nach dem selben Grenzwertbegriff, nach dem auch

gilt.
Das ist ein völlig korrekte Aussage in der derzeitigen, zu oberflächlichen Mathematik, behaftet mit dem Fehler, daß

keine Zahl ist und dreimal nicht eine natürliche, weshalb schon diese Formulierung des Grenzwertes einen inneren formalen Widerspruch aufweist und somit falsch ist.
n, eine natürliche Zahl, kann nicht gegen Unendlich streben, sondern nur die Menge der natürlichen Zahlen durchlaufen, in welcher Unendlich nicht enthalten ist!

ist also eine mathematisch nicht nur unexakte, sondern schlichtweg falsche Formulierung.
Sie müßte wahrheitsgemäß lauten

q.e.d.
Sprüche 14,13
Auch beim Lachen kann das Herz sich grämen,
und das Ende der Freude ist Leid.
Re: Existenz größter und kleinster Zahlen
Verfasst: Sonntag 13. September 2009, 21:58
von Todoroff
Trockennasenaffe RPL32P12
Die Gleichheit von 1 und 0,999... können Sie gar nicht ad absurdum führen, ohne gegen das archimedische Axiom zu verstoßen.
Das da lautet?
In der gegenwärtigen Mathematik ist wünschenswert, dass es keine kleinste positive reelle Zahl gibt, deswegen wird das archimedische Axiom angenommen.
Begründung!
Sprüche 14,14
Für seinen Wandel empfängt der Abtrünnige Vergeltung,
und so auch der Gute für seine Taten.
Re: Existenz größter und kleinster Zahlen
Verfasst: Sonntag 13. September 2009, 22:20
von Todoroff
Trockennasenaffe RPL32P12
Das ist die Formulierung:
Eine reelle Zahl b ist Grenzwert der Folge reeller Zahlen
)
, wenn gilt:
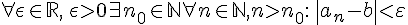
(Mit den reellen Zahlen als vollständiger archimedischer angeordneter Körper und natürlichen Zahlen, welche den Paeno-Axiomen entsprechen).
Wo steckt der Widerspruch?
Es heißt Peano und nicht Paeno.
Dieser, von mir so getaufte, Epsilon-Beweis gilt nur im Endlichen. Es ist Unmöglich, im Abzählbaren Summen oder Differenzen zu bilden.
Todoroff hat geschrieben: n, eine natürliche Zahl, kann nicht gegen Unendlich streben, sondern nur die Menge der natürlichen Zahlen durchlaufen, in welcher Unendlich nicht enthalten ist!

ist also eine mathematisch nicht nur unexakte, sondern schlichtweg falsche Formulierung.
Sie müßte wahrheitsgemäß lauten

Was ist das jetzt für ein Unsinn?
Dieser "Unsinn" ist nur ein mathematisch präzise(re) Formulierung.
Zum einen, das ist
nicht die Formulierung.
So, so, kann man in Ihrer komischen Mathematik jetzt keine Grenzwerte mehr bilden = LIMES-Operationen durchführen?
Und zum anderen kann auch schreiben
 Korrekt
Korrekt
Und die Aussage ist noch immer die selbe, solange sich nicht geändert hat, was lim bedeutet.
Korrekt. Aber mit dem Buchstaben n wird in aller Regel ein Element der Menge der natürlichen Zahlen N bezeichnet.
Also, Herr Todororff, was bedeutet

innerhalb der gegenwärtigen Mathematik (nein, ich frage nicht danach, wie Sie das definieren, sondern wie die gegenwärtige Mathematik das definiert)?
Die herrschende Mathematik erklärt hier, daß eine UNENDLICHE Zahlenfolge, dies nicht gibt, nicht geben kann, was Sie zu begreifen sich weigern, dem Wert z entgegenstrebt und im Grenzfall dem Zahlenwert z gleich ist, weil der Abstand Null geworden ist im Unendlichen.
Hebr 10,35-36
Darum werft euer Vertrauen nicht weg, welches eine große Belohnung hat. Geduld aber habt ihr nötig, damit ihr den Willen Gottes tut und das Verheißene empfangt.
Ich danke Ihnen, mich mit Ihnen in Geduld üben zu dürfen.
Re: Existenz größter und kleinster Zahlen
Verfasst: Sonntag 13. September 2009, 22:29
von Todoroff
Mileva
Der Epsilon-Beweis belegt nicht, dass sich keine zwei Zahlen finden lassen, zwischen die sich kein Epsilon als dritte reelle Zahl schieben lässt, sondern: In einem offenen Intervall lassen sich keine zwei Zahlen ausfindig machen,
Präziser:
NUR in dem offenen Intervall (0,1) lasse sich nicht zwei Zahlen finden, zwischen die keine dritte geschoben werden kann. Das ist schon falsch im geschlossenen Intervall [0,1], weshalb das ganze eine Mogelpackung ist.
Die Liebe ist die Selbsterkenntnis des Lebens.
Allein in der Liebe vermag sich das Leben zu erkennen.
Ein Leben ohne Liebe ist ein erkenntnisloses Leben,
ein bloßes Sein - das ist der Tod.
Georg Todoroff
Re: Existenz größter und kleinster Zahlen
Verfasst: Sonntag 13. September 2009, 22:56
von Todoroff
Trockennasenaffe RPL32P12
Die Gleichheit von 1 und 0,999... können Sie gar nicht ad absurdum führen, ohne gegen das archimedische Axiom zu verstoßen.
Das da lautet?
Schauen Sie in das Thema "Definition Grenzwert", das hab ich Ihnen alles schon erzählt.
DAU-Niveau.
Todoroff hat geschrieben:In der gegenwärtigen Mathematik ist wünschenswert, dass es keine kleinste positive reelle Zahl gibt, deswegen wird das archimedische Axiom angenommen.
Begründung!
Sie wollen eine Begründung dafür, warum die Mathematiker keine kleinste positive reelle Zahl haben möchten?
Ganz einfach, lässt man solche Zahlen in den reellen Zahlen zu, dann geht der gesamte Grenzwertbegriff in die Binsen.
Fast korrekt. Letztlich betrifft es nur den Epsilon-Beweis, der neu formuliert werden müßte. Wahrheit aber ist unabhängig vom Willen des Menschen. Die Physiker wollen auch nicht die Einführung des Lichtäthers, weil das zur Konsequenz hätte eine völlig neue, grundlegend veränderte Beschreibung des Weltalls, des sogenannten Naturgeschehens und stürzen so die Menschheit aufgrund ihrer Faulheit und Denkträgheit in den Untergang, so wie Sie, denn der Genzwert, um welchen es hier geht:
>0)
ist die mathematische Beschreibung eines Elementes des Lichtäthers, und das rettet VIELLEICHT das Überleben der Menschheit, also auch Ihres.
Glauben Sie mir eigentlich mittlerweile, dass die Folge ((1+1)^1, (1+1/2)^2, (1+1/3)^3, (1+1/4)^4, ...) monoton steigend ist?
Gehört nicht zum Thema. Sie ist im Endlichen monoton steigend, um im Abzählbaren auf den Zahlwert 1 zu fallen aufgrund der hier diskutierten Problematik, nämlich der falschen Behauptung
=0)
womit Sie einen wunderschönen Beweis für Ihr falschen Gedankengänge geliefert haben, welche denen der herrschenden Mathematik identisch sind.
q.e.d.
Hebr 12,11
Jede Züchtigung aber, wenn sie da ist, scheint uns nicht Freude, sondern Leid zu sein; danach aber bringt sie als Frucht denen, die dadurch geübt sind, Frieden und Gerechtigkeit.
Re: Existenz größter und kleinster Zahlen
Verfasst: Sonntag 13. September 2009, 23:08
von Todoroff
Trockennasenaffe RPL32P12
Dieser, von mir so getaufte, Epsilon-Beweis gilt nur im Endlichen. Es ist Unmöglich, im Abzählbaren Summen oder Differenzen zu bilden.
Prima dass sämtliche Zahlen, die da vorkommen, endlich sind.
Du nixe begreifen, DAU. Die Menge der natürlichen Zahlen besteht nur aus endlich vielen Zahlen mit einer endlichen Ziffernfolge und aus abzählbar vielen mit einer abzählbaren Ziffernfolge.
Verstehen Sie nicht, dass das hinschreiben von den drei Buchstaben lim etwas anderes ist, als die Definition des Grenzwerts?
Komisch, bisher behaupteten Sie immer das Gegenteil. Wie lautet Ihre Entscheidung?
Todoroff hat geschrieben:Also, Herr Todororff, was bedeutet

innerhalb der gegenwärtigen Mathematik (nein, ich frage nicht danach, wie Sie das definieren, sondern wie die gegenwärtige Mathematik das definiert)?
Die herrschende Mathematik erklärt hier, daß eine UNENDLICHE Zahlenfolge, dies nicht gibt, nicht geben kann, was Sie zu begreifen sich weigern, dem Wert z entgegenstrebt und im Grenzfall dem Zahlenwert z gleich ist, weil der Abstand Null geworden ist im Unendlichen.
Anscheinend wissen Sie wirklich nicht, wie es in der gegenwärtigen Mathematik definiert ist.
Dafür haben wir doch Sie, einen DAU!
Sprüche 14,12
Mancher Weg erscheint einem eben;
doch das Ende davon sind Pfade des Todes.
Re: Existenz größter und kleinster Zahlen
Verfasst: Montag 14. September 2009, 12:16
von Todoroff
DAU RPL32P12
Ich hab die Peano-Axiome vorausgesetzt, nach denen gibt es nur endliche natürliche Zahlen.
Wenn Sie falsche Voraussetzungen treffen, ist das doch allein Ihr Problem. So liefern Sie uns ein schönes Beispiel für die Falschheit von Axiomen.
Wie lösen Sie den Widerspruch auf:
N enthält nur Zahlen mit endlichen Ziffernfolgen
und
N ist abzählbar unendlich?
Wenn ich die Peano-Axiome voraussetze sind alle meine natürlichen Zahlen endlich.
Korrekt, aber falsche Voraussetzung, DAU.
Einer spinnt immer!
Heute sind Sie dran.
Für Sie, DAU, ist HEUTE jeder Tag.
Re: Existenz größter und kleinster Zahlen
Verfasst: Montag 14. September 2009, 12:36
von Todoroff
Trockennasenaffe Cdh
Was bringt ...999 in der Praxis?
Nimmt diese Folge ihren Grenzwert tatsächlich an?
Würde das Einsetzen dieser Zahl exakt die Eulersche Zahl liefern?
^{...999}=e) Korrekt.
Korrekt.
..999,0 steht in unmittelbarem Zusammenhang mit 1-0,999..., was mathematisch ein Urteilchen beschreibt, das Element des Lichtäthers, und damit das Lügengebäude Einsteins stürzt, was der Menschheit das Überleben sichern könnte (aus der Sicht der Gottlosen).
Ps 9,10-11
Der Herr wird den Bedrückten zum Hort,
zum Hort für die Zeiten der Drangsal.
Drum vertrauen dir, die deinen Namen kennen;
Denn die dich suchen, o Herr, die verlässest du nicht.
Re: Existenz größter und kleinster Zahlen
Verfasst: Montag 14. September 2009, 12:45
von Todoroff
Trockennasenaffe Cdh
Ich habe ausgeführt, dass 1/n in einer Folge nicht Null WIRD, dass es aber 0 als Grenze hat. Der limes gibt nicht den Wert an, den eine Folge annimmt, der limes gibt den Wert der Grenze an. Und die Grenze ist 0.
Falsch. Die Grenze ist der Nachfolger von Null.
Die Folge selbst kommt beliebig nahe an die Grenze heran, bleibt aber immer davon verschieden.
korrekt.
Einer mit EINER Uhr weiß immer, wie spät es ist.
Einer mit zwei Uhren ist sich nie sicher!
Re: Existenz größter und kleinster Zahlen
Verfasst: Montag 14. September 2009, 13:21
von irgendwer
N enthält nur Zahlen mit endlichen Ziffernfolgen
und
N ist abzählbar unendlich?
Lieber Herr Todoroff:
Wo liegt denn da bitte der Widerspruch?
Es gibt (abzählbar) unendlich viele Zahlen mit endlich vielen Ziffern!!!
Liebe Grüsse
Ihr Freund und Bruder
Irgendwer
Re: Existenz größter und kleinster Zahlen
Verfasst: Montag 14. September 2009, 21:19
von Todoroff
irgendwer
Zurück aus dem Urlaub?
N enthält nur Zahlen mit endlichen Ziffernfolgen
und
N ist abzählbar unendlich?
Es gibt (abzählbar) unendlich viele Zahlen mit endlich vielen Ziffern!!!
Falsch!
Wievielstellig ist

Sprüche 16,21
Wer weisen Sinns ist, wird verständig gepriesen;
und freundliche Rede fördert die Belehrung.
Re: Existenz größter und kleinster Zahlen
Verfasst: Montag 14. September 2009, 21:35
von Linn
Lieber Herr Todoroff,
Sie haben in Ihrer "neuen Mathematik" herausgestellt, dass


sei. Mein Taschenrechner bestätigt dies zwar nicht, aber wenn das tatsächlich zutreffend ist, welches Ergebnis erhalte ich denn stattdessen aus der Division

oder aus

?
Ich weiß, die Frage wurde bereits gestellt, aber ich habe Ihre Antwort darauf noch nicht gefunden. Für wichtig halte ich die Beantwortung aber vor allem deswegen, weil ich finde, dass Ihre "neue Mathematik" in der Lage sein muss, eine schlüssige Division wie

zu ermöglichen.
Vielen Dank und schöne Grüße
Linn
Re: Existenz größter und kleinster Zahlen
Verfasst: Montag 14. September 2009, 21:42
von Todoroff
Trockennasenaffe RPL32P12
Wenn Sie falsche Voraussetzungen treffen, ist das doch allein Ihr Problem. So liefern Sie uns ein schönes Beispiel für die Falschheit von Axiomen.
Wie lösen Sie den Widerspruch auf:
N enthält nur Zahlen mit endlichen Ziffernfolgen
und
N ist abzählbar unendlich?
Wo ist der Widerspruch? Wenn

nur Zahlen enthält, die aus n Ziffern mit

bestehen, dann enthält

doch sogar schon nicht-endlich viele Zahlen mit einer verschiedenen Anzahl von Ziffern.
Sie sind eben ein DAU. Eine nicht endliche Zahl von Zahlen in N ist nur zu erreichen über eine nicht-endliche Zahl von Ziffern einer Zahl, denn jede Zahl in N gibt ja an, die wievielte Zahl in N sie ist. So ist 100 die hundertste Zahl in N und die "nicht-endlichste" diejenige mit einer nicht-endlichen Ziffernfolge.
q.e.d.
Jede natürliche Zahl ist endlich.
Falsch!
Die Menge der natürlichen Zahlen ist keine endliche Menge, da es echte Teilmengen von

gibt, welche die gleiche Mächtigkeit wie

besitzen.
Korrekt, davon gibt es aber nur endlich viele, nicht abzählbar viele abzählbare Mengen als echte Teilmengen in N.
Die endliche Vereinigung von abzählbaren Mengen ist abzählbar, nach CANTOR sogar die abzählbare Vereinigung von abzählbaren Mengen, was ich widerlegt habe.
Mal ein paar Definitionen zu endlichen Zahlen.
Setze: 0 ist endlich.
Setze: Wenn ich zu einer endlichen Zahl 1 addiere, erhalte ich eine endliche Zahl.
Nur im Endlichen.
Ich denke, der ersten Definition werden Sie nicht widersprechen wollen. Falls Sie der zweiten Definition widersprechen wollen, so bedenken Sie vorher: Wenn es eine endliche Zahl gibt, so dass man wenn man zu dieser Zahl 1 addiert, eine nicht-endliche zahl erhält, so ist diese Zahl größer, als jede andere endliche Zahl, was zumindest meiner Vorstellung einer endlichen Zahl widerspricht.
Ihr mangelhaftes Vorstellungsvermögen ist die Ursache, dafür, daß Sie dieses Thema hoffnungslos überfordert. Einfach aufgeben.
Setzt man diese Definitionen vorraus, so folgt mit dem Induktionsaxiom aus den Peano-Axiomen sofort, dass jede natürliche Zahl endlich ist.
Sie kapieren es nicht. Das gilt alles nur im Endlichen. Es ist unmöglich, die Gesetzmäßigkeiten des Endlichen zu übertragen auf das Unendliche. Das wissen Sie selbst.
Wenn ich die Peano-Axiome voraussetze sind alle meine natürlichen Zahlen endlich.
Das interessiert doch keinen.
Welche Vorraussetzungen ich benutze, wenn ich Mathematik betreibe bleibt mir überlassen, solange keine Widersprüche existieren.
Sie dürfen gern Ihre eigene Mathematik betreiben - interessiert hier keinen. Sie sollten aber nicht so unglaublich verlogen sein, mir vorzuwerfen,was Sie selbst tun. Ihr Gottlosen seid eben einfach nur das nackte Grauen.
Sprüche 16,22
Wer Verstand besitzt, dem ist er ein Lebensquell;
die Strafe der Toren ist die Torheit selbst.