1 - 0,999... = 0 ?

[LaughingMan]

Herr Todoroff.
Ich muss zugeben, dass ich eigentlich gar nicht mit Ihnen diskutieren wolte (wir hatten das alles schon), aber da Mileva keine offene Diskussion führen möchte, hab ich ja ein wenig Zeit übrig. (Und ich muss zugeben, dass es mir Spaß macht.)

Zum Einen haben sie diese Widersprüche (besonders 2. und 3.) seit 31 Monaten nicht geklärt. Ich vemute aber, dass ihre Antwort hierauf aus höchstens zwei Zeilen besteht und keine mathematischen Formulierungen enthalten wird.

Deswegen zu ...999,0, denn das liegt ihnen wohl mehr.

LaughingMan
Die verschiedenen Probleme mit ...999,0 in Verbindung mit den Axiomen der natürlichen Zahlen wurden wiederholt dargelegt.
Diese Probleme hat nicht die Mathematik, sondern nur ihr Gottlosen, weil ihr nicht bis Zwei zählen könnt, und deshalb Unfug konstruiert und behauptet.

Nochmal in kurz: Die natürlichen Zahlen sind nicht auf eine schwammige Art und Weise "irgendwie so wie das Zählen" definiert, sondern sind genau die Menge, die von den Peano-Axiomen erzeugt wird (bzw. ist isomorph zu allen so erzeugten Mengen):

1. 1 ist eine natürliche Zahl.
2. Zu jeder natürlichen Zahl n gibt es genau einen Nachfolger n', der ebenfalls eine natürliche Zahl ist.
3. Es gibt keine natürliche Zahl, deren Nachfolger 1 ist.
4. Jede natürliche Zahl ist Nachfolger höchstens einer natürlichen Zahl.
5. Von allen Mengen X, welche
   • die Zahl 1 und
   • mit jeder natürlichen Zahl n auch stets deren Nachfolger n'
   enthalten, ist die Menge der natürlichen Zahlen die kleinste.

...999,0 lässt sich damit nicht in Einklang bringen! Wenn Sie das bestreiten wollen, geben sie bitte den Nachfolger an.

Auf Ihrer Homepage verschleiern Sie das Problem mit dem Nachfolger, indem sie 1 addieren und dabei irgendwie so ein wenig 0 erhalten (aber auch nicht so richtig). Es sei aber festgehalten, dass Sie wieder mal nicht mathematisch korrekt vorgehen, denn die Addition ist innerhalb der natürlichen Zahlen über die Nachfolgerfunktion definiert!
Statt also umständlich und erfolglos 1 zu addieren, müssten Sie den Nachfolger definieren - nennen wir ihn . Dann ergibt die Definition der Addition automatisch ...999,0 + 1 = .


Innerhalb der Mathematik wird übrigens an keiner Stelle behauptet die natürlichen Zahlen seien die Zahlenmenge zum korrekten Widerspiegeln der Realität. Wenn Sie meinen in der Realität lässt sich eine größte Zahl finden (entschuldigen Sie die flachse Formulierung), steht das in keinem Widerspruch zu den natürlichen Zahlen - diese sind dann einfach nicht die geeignete Menge, um z.B. zu zählen.
Wenn sie zum Rechnen und Beweisen also eine Menge von Zahlen brauchen, die ein größtes Element enthält, sollten Sie sich diese Menge einfach definieren und schon kann's losgehen. Aber:

1. Dazu brauchen sie ein Axiomensystem.
2. Nennen Sie diese Menge nicht die natürlichen Zahlen, denn die gibt's schon und sie sind mit einer größten Zahl nicht vereinbar (siehe oben). Sie könnten sie z.B. die Echten Zahlen nennen.

[Todoroff]

LaughingMan
Zum Einen haben sie diese Widersprüche (besonders 2. und 3.) seit 31 Monaten nicht geklärt.
Das ist Ihr Glaube. Ich beantworte keine Fragen, die keiner Antwort bedürfen und nur beweisen, daß der Fragende die Problemstellung nicht erfaßt hat.

Deswegen zu ...999,0, denn das liegt ihnen wohl mehr.
Ihr Zuvorkommen ist geradezu bewunderungswürdig. Und was liegt Ihnen? Bisher vermag ich nichts zu erkennen, außer Dummschwätzerei.

Nochmal in kurz: Die natürlichen Zahlen sind nicht auf eine schwammige Art und Weise "irgendwie so wie das Zählen" definiert, sondern sind genau die Menge, die von den Peano-Axiomen erzeugt wird (bzw. ist isomorph zu allen so erzeugten Mengen):

1. 1 ist eine natürliche Zahl.
2. Zu jeder natürlichen Zahl n gibt es genau einen Nachfolger n', der ebenfalls eine natürliche Zahl ist.
3. Es gibt keine natürliche Zahl, deren Nachfolger 1 ist.
   Das ist umstritten und eine philosophische Frage. Ich definiere: Null ist eine natürliche Zahl, aus philosophischen Gründen.
4. Jede natürliche Zahl ist Nachfolger höchstens einer natürlichen Zahl.
5. Von allen Mengen X, welche
   • die Zahl 1 und
   • mit jeder natürlichen Zahl n auch stets deren Nachfolger n'
   enthalten, ist die Menge der natürlichen Zahlen die kleinste.

...999,0 lässt sich damit nicht in Einklang bringen! Wenn Sie das bestreiten wollen, geben sie bitte den Nachfolger an.
Der Nachfolger ist Null.

Auf Ihrer Homepage verschleiern Sie das Problem mit dem Nachfolger, indem sie 1 addieren und dabei irgendwie so ein wenig 0 erhalten (aber auch nicht so richtig).
Das überfordert Sie.

Es sei aber festgehalten, dass Sie wieder mal nicht mathematisch korrekt vorgehen, denn die Addition ist innerhalb der natürlichen Zahlen über die Nachfolgerfunktion definiert!
Statt also umständlich und erfolglos 1 zu addieren, müssten Sie den Nachfolger definieren - nennen wir ihn . Dann ergibt die Definition der Addition automatisch ...999,0 + 1 = .
Unfug.
Die Zahl ...999,0 ist nur zu denken, also nicht wirklich eine Zahl, wie wie sie aus dem Endlichen kennen sondern ein Prozeß, ein nie endender Prozeß. Das überfordert Sie einfach bloß, weshalb Sie hier nicht schreiben sollten.



Innerhalb der Mathematik wird übrigens an keiner Stelle behauptet die natürlichen Zahlen seien die Zahlenmenge zum korrekten Widerspiegeln der Realität.
Das ist nur Dummschwätzerei. DIE Mathematik gibt es gar nicht. Sie entwickelt sich so, wie wir Menschen uns entwickeln. Das überfordert solche Kleingeister wie Sie.
Wie alt sind Sie?
Welchen Beruf üben Sie aus?
Welchen Bildungshintergrund haben Sie?

Wenn Sie meinen in der Realität lässt sich eine größte Zahl finden (entschuldigen Sie die flachse Formulierung), steht das in keinem Widerspruch zu den natürlichen Zahlen
korrekt

- diese sind dann einfach nicht die geeignete Menge, um z.B. zu zählen.
sondern welche Menge wollen Sie zum Zählen einführen?

Wenn sie zum Rechnen und Beweisen also eine Menge von Zahlen brauchen, die ein größtes Element enthält, sollten Sie sich diese Menge einfach definieren und schon kann's losgehen.
Dummschwätzerei

Aber:

1. Dazu brauchen sie ein Axiomensystem.
2. Nennen Sie diese Menge nicht die natürlichen Zahlen, denn die gibt's schon
   Ach, das wußte ich gar nicht.
   
   und sie sind mit einer größten Zahl nicht vereinbar (siehe oben).
   Und das behauptet kleines dummes Besserwisserchen, der nix verstanden hat. Toll.
   Da bin ich doch begeistert von solchen Klugscheißern.
   
   Sie könnten sie z.B. die Echten Zahlen nennen.
   Das ist eine mir unbekannt Menge. Wie heißt die Menge der unechten Zahlen?
   
   Hes 34,11
   So spricht Gott, der Herr: Jetzt will Ich Meine Schafe Selber suchen und Mich Selber um sie kümmern.

[LaughingMan]

Aber, aber Herr Todoroff.

Keine sachliche Argumentation? Von jemandem, der sein Diplom scheinbar vor der Einführung der Axiomatisierung gemacht hat, sind das mutige Worte. Und von Selbstgerechtigkeit zeugen sie, wenn eine "Antwort" so aussieht:

Das ist Ihr Glaube. Ich beantworte keine Fragen, die keiner Antwort bedürfen und nur beweisen, daß der Fragende die Problemstellung nicht erfaßt hat.

Und was liegt Ihnen? Bisher vermag ich nichts zu erkennen, außer Dummschwätzerei.

Das ist umstritten und eine philosophische Frage.

Das überfordert Sie.

Die Zahl ...999,0 ist nur zu denken, also nicht wirklich eine Zahl, wie wie sie aus dem Endlichen kennen sondern ein Prozeß, ein nie endender Prozeß. Das überfordert Sie einfach bloß, weshalb Sie hier nicht schreiben sollten.

Das ist nur Dummschwätzerei. DIE Mathematik gibt es gar nicht. Sie entwickelt sich so, wie wir Menschen uns entwickeln. Das überfordert solche Kleingeister wie Sie.

Dummschwätzerei

Ach, das wußte ich gar nicht.

Und das behauptet kleines dummes Besserwisserchen, der nix verstanden hat. Toll.
Da bin ich doch begeistert von solchen Klugscheißern.

Ich hatte mich bis jetzt nicht mit Alter, Bildungshintergrund und Beruf vorgestellt, weil ich diese Fakten für unnötig halte. Jeder Mitlesende sollte sich seine Meinung unabhängig von Autoritäten bilden und lieber den Verstand dazu benutzen, die Argumentation mit zu verfolgen.
Da Sie aber vermutlich jede weitere Bloßstellung von Widersprüchen ihrer Argumente löschen werden, will ich Ihnen den Gefallen tun.

Ich bin 32 Jahre alt und habe das Mathematikstudium vor sechs Jahren erfolgreich beendet. Nach zwei Jahren außeruniversitärer Beschäftigung schreibe ich gerade meine Doktorarbeit in der Informatik (genauer: an der Schnittstelle Logik/Informatik) zu Ende. Angestellt bin ich eben als Doktorand der Universität.

Irritierend finde ich allerdings, dass gerade Sie so sehr auf die Autorität einer offiziellen Einrichtung pochen. Sie können keine Bildung in den Bereichen Physik, Biologie, Philosophie oder Religion nachweisen und dennoch hat Ihnen dafür nie jemand die Fähigkeit abgesprochen, diese Themen zu diskutieren.
An einer sachbezogene Diskussion kann sich jeder beteiligen, so lange er logisch korrekte Schlüsse zieht und dazu nur akzeptierte Fakten verwendet. Genau das tat ich in dem gelöschten Post und die Tatsache, dass darin einmal mehr ihre Theorie von einer größten Zahl als unvereinbar mit den natürlichen Zahlen, wie sie durch die Peano-Axiome erzeugt werden, nachgewiesen wird, hat wohl eher zur Löschung geführt, als Ihr Interesse an meinem Lebenslauf.
Aber da wir das jetzt geklärt haben, können wir ja wieder zurück zur Materie kehren:

Die Kurzfassung ist ganz einfach:

1. Die natürlichen Zahlen (wahlweise mit Null oder ohne ) sind als genau die Menge definiert, welche von den Peano-Axiome erzeugt wird.
2. Eine Menge, die den Peano-Axiomen nicht gehorcht, ist also nicht die gleiche wie die natürlichen Zahlen.
3. ...999,0 (mit Nachfolger 0) widerspricht (in obiger Nummerierung mit "0" statt "1" - Vergleiche hier) Axiom 3, denn dann gibt es einen Vorgänger von 0.
4. Also ist keine Menge, die ...999,0 enthält, die gleiche wie .

Ich warte weiterhin auf Gegenargumente...

Einen Ausweg habe ich ihnen auch schon aufgezeigt:
Definieren Sie eine neue Menge (am besten mit einer Verknüpfung darauf).

[Todoroff]

LaughingMan
Ich hatte mich bis jetzt nicht mit Alter, Bildungshintergrund und Beruf vorgestellt, weil ich diese Fakten für unnötig halte.
Das dürfen Sie glauben - ich halte es für nötig (bei diesem Thema).

Da Sie aber vermutlich jede weitere Bloßstellung von Widersprüchen ihrer Argumente löschen werden, will ich Ihnen den Gefallen tun.
Das ist bloß albern. Sie haben bisher keine Widersprüche gefunden, sondern nur geglaubt, Sie hätten welche gefunden, was andere nicht beurteilen können, die sich auf diesem Gebiet nicht auskennen, womit Sie mir bewiesen haben, daß Sie das Thema überfordert. Ich bin weiterhin der Überzeugung, daß 90% der Mathematiker bei diesem Thema aussteigen, was mich die Erfahrung lehrt.

Ich bin 32 Jahre alt und habe das Mathematikstudium vor sechs Jahren erfolgreich beendet. Nach zwei Jahren außeruniversitärer Beschäftigung schreibe ich gerade meine Doktorarbeit in der Informatik (genauer: an der Schnittstelle Logik/Informatik) zu Ende. Angestellt bin ich eben als Doktorand der Universität.
Hört sich doch mal gut. Nun zeigen Sie uns auch mal, was Sie drauf haben und zählen bis Zwei.

An einer sachbezogene Diskussion kann sich jeder beteiligen, so lange er logisch korrekte Schlüsse zieht
Korrekt, aber genau das könnt ihr Gottlosen eben nicht, sondern nur Glaubensbekenntnisse absondern.

und dazu nur akzeptierte Fakten verwendet. Genau das tat ich in dem gelöschten Post
Das mag ja Ihr Glaube sein - aus meiner Sicht war es eben nicht so. Ihr Geschreibsel hat nur davon gezeugt, daß Sie das Problem nicht erfaßt haben - wie dann die Beweisführung?

und die Tatsache, dass darin einmal mehr ihre Theorie von einer größten Zahl als unvereinbar mit den natürlichen Zahlen, wie sie durch die Peano-Axiome erzeugt werden,
Auch das ist nur Ihr (falscher) Glaube - Sie haben es eben nicht nachweisen können (nur unter Voraussetzung der Unkenntnis meiner Beweise, die das eben alles widerlegen).

nachgewiesen wird, hat wohl eher zur Löschung geführt, als Ihr Interesse an meinem Lebenslauf.
Glauben Sie es, wenn es Sie glücklich macht.

Die Kurzfassung ist ganz einfach:

1. Die natürlichen Zahlen (wahlweise mit Null oder ohne ) sind als genau die Menge definiert, welche von den Peano-Axiome erzeugt wird.
2. Eine Menge, die den Peano-Axiomen nicht gehorcht, ist also nicht die gleiche wie die natürlichen Zahlen.
3. ...999,0 (mit Nachfolger 0) widerspricht (in obiger Nummerierung mit "0" statt "1" - Vergleiche hier) Axiom 3, denn dann gibt es einen Vorgänger von 0.
   Hören Sie auf mit solchen Verweisen. Dann reicht es mir nämlich auch, nur immer auf meine HP und meine Bücher zu verweisen. Wie will man dann argumentieren? Sie argumentieren WIEDERHOLT nicht und SIE sind es, der die Probleme hat, nicht ich.
4. Also ist keine Menge, die ...999,0 enthält, die gleiche wie .

Das bleibt einfach Unfug.
Indem Sie solches (wiederholt) behaupten, erklären Sie WIEDERHOLT, daß Sie das Problem nicht erfaßt haben.
Nennen Sie die letzte Zahl in der Menge von N.
Können Sie selbige nicht benennen, können Sie solchen Unfug auch nicht behaupten.
Ich warte weiterhin auf Gegenargumente...
Ich lese nicht EIN Argument.
Wer legt fest, welchen Axiomen die Menge N zu genügen hat?
Die mathematische Fachwelt ist der Überzeugung, daß die CANTORschen Diagonalverfahren richtig sind und ich beweise, daß sie falsch sind. Und jetzt?
Was ist Wahrheit? Welcher Gott in Menschengestalt erklärt, daß es so und nicht anders zu sein hat?
Die Masse HAT immer recht, aber noch NIE war sie IM Recht.

Einen Ausweg habe ich ihnen auch schon aufgezeigt:
Definieren Sie eine neue Menge (am besten mit einer Verknüpfung darauf).Das ist der abermalige Beweis, daß Sie das Problem nicht verstanden haben. Und ich bin schuld, wenn Sie zu dämlich dafür sind? So erbärmlich seid ihr Gottlosen eben.

Jede Krise hat nicht nur ihre Gefahren, sondern auch ihre Möglichkeiten.
Jede kann Heil oder Untergang bedeuten.
Martin Luther King

Fortschritts-Blockierer wie Sie bewirken mit ihrer Denk-Unfähigkeit den Untergang. Sie gehören zu jenen, die von der Geschichte einfach überrollt werden müssen.

[LaughingMan]

An einer sachbezogene Diskussion kann sich jeder beteiligen, so lange er logisch korrekte Schlüsse zieht
Korrekt, aber genau das könnt ihr Gottlosen eben nicht, sondern nur Glaubensbekenntnisse absondern.

und dazu nur akzeptierte Fakten verwendet. Genau das tat ich in dem gelöschten Post
Das mag ja Ihr Glaube sein - aus meiner Sicht war es eben nicht so. Ihr Geschreibsel hat nur davon gezeugt, daß Sie das Problem nicht erfaßt haben - wie dann die Beweisführung?

[...]

und die Tatsache, dass darin einmal mehr ihre Theorie von einer größten Zahl als unvereinbar mit den natürlichen Zahlen, wie sie durch die Peano-Axiome erzeugt werden,
Auch das ist nur Ihr (falscher) Glaube - Sie haben es eben nicht nachweisen können (nur unter Voraussetzung der Unkenntnis meiner Beweise, die das eben alles widerlegen).

Sie gehen noch immer davon aus, dass wir über Ihre Beweise diskutieren, aber das stimmt nicht. Es geht einzig und allein darum, dass eine größte natürliche Zahl nicht mit den Peano-Axiomen vereinbar ist. Dazu bedarf es nicht der Diskussion über irgendeinen Beweis!

Als konkretes Beispiel: Wenn ich behaupte, 10 sei keine gerade Zahl, lässt sich das auch ohne Betrachtung dessen, was ich für einen Beweis halte, widerlegen, indem man 10 durch 2 teilt und keinen Rest erhält. DAS widerlegt meinen Beweis und keine Betrachtung des selbigen.
Im Allgemeinen: Es ist unnötig, einen einen Beweis zu einer Behauptung zu verstehen und einen einzelnen Beweisschritt zu falsifizieren, falls man schon die Aussage der Behauptung zu einem Widerspruch führen kann. Dann kann die Behauptung - und damit der Beweis - nicht korrekt sein.

So auch hier: ...999,0 widerspricht den Peano-Axiomen und ist damit nicht in der Menge enthalten, die durch diese erzeugt wird.

Hören Sie auf mit solchen Verweisen. Dann reicht es mir nämlich auch, nur immer auf meine HP [...] zu verweisen.

Das machen Sie doch ständig! Sie unterlassen es regelmäßig, echte Gegenargumente zu bringen und behaupten statt dessen, all dies sei schon diskutiert oder auf ihrer HP geschrieben worden. Selbstverständlich ohne jemals den genauen Ort zu spezifizieren.
Ein gutes Beispiel ist der , der auf ihrer HP mehrfach verwendet, aber nie definiert wurde. Auf Nachfragen reagierten Sie bis jetzt ausschließlich mit Verweisen und nie mit der Angabe einer konkreten Definition.

Wie will man dann argumentieren? Sie argumentieren WIEDERHOLT nicht und SIE sind es, der die Probleme hat, nicht ich.

Ich erkläre Ihnen gerne nochmal, wie man argumentiert:
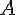
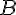
Prinzipiell ist dafür der Modus Ponens geeignet, der für zwei Aussagen und so funktioniert:
.
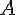
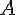
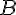
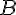
Weiß man also, dass stimmt und aus folgt, weiß man, dass auch gilt.
Um mit dem logischen Schließen los zu legen, benötigt man also mindestens eine wahre Aussage. Nun kann man die aber nicht auf diese Art beweisen und man steckt irgendwie fest. Eine seither praktizierte Lösung - die Axiomatisierung - fand vor etwa 2300 Jahren Euklid.
Seitdem beginnt man, indem man einige Dinge einfach als wahr annimmt (eben die Axiome) und mit diesen Aussagen das logische Schließen beginnt.

Und genau hier ist Ihr Problem: Ihre natuerlichen Zahlen, entsprechen nicht den Peano-Axiomen, denn sie widersprechen mindestens einem davon.
Nun sind die Peano-Axiome natürlich nicht das einzig Wahrheit-stiftende und deswegen ist das nicht weiter tragisch. Aber damit sind selbstverständlich alle Sätze, die für die natürlichen Zahlen gelten erst einmal ungültig, denn sie stützen sich ja gerade auf diese Axiome. Auch das ist nicht weiter tragisch, denn man kann ja neue und andere Sätze beweisen. Ein gutes Beispiel dafür sind die rationalen und reellen, die nicht den Peano-Axiomen gehorchen, aber dennoch jede Menge interessanter Eigenschaften haben.
Wenn also andere Axiome gelten, ist das kein Beinbruch, man darf dann nur nicht mehr - und das machen Sie ständig - die Eigenschaften verwenden, die mit eben diesen Axiomen bewiesen wurden!

Also ist keine Menge, die ...999,0 enthält, die gleiche wie .
Das bleibt einfach Unfug.
Indem Sie solches (wiederholt) behaupten, erklären Sie WIEDERHOLT, daß Sie das Problem nicht erfaßt haben.
Nennen Sie die letzte Zahl in der Menge von N.
Können Sie selbige nicht benennen, können Sie solchen Unfug auch nicht behaupten.

Und noch einmal: Es gibt keine letzte (ich interpretiere das mal als "größte") Zahl in !

Ich lese nicht EIN Argument.
Wer legt fest, welchen Axiomen die Menge N zu genügen hat?

Konsens. Und zwar nicht, weil die Mehrheit Recht hat oder ähnlich obskure und zweifelhafte Gründe, sondern einfach nur, weil es die Diskussion einfacher macht, wenn mit dem Begriff "natürliche Zahlen" (bzw. , ) alle das gleiche meinen.
Denn um nichts mehr handelt es sich bei den Worten "natürliche Zahlen" - es ist ein Begriff! Ihm wohnt keine innere wahrheitspendende Bedeutung inne. Es handelt sich einfach nur um einen Namen für die Menge, die durch die Peano-Axiome erzeugt wird! Die Axiome sind es, die jeden weiteren Schluss erlauben. Deswegen wiegt Ihr Widerspruch zu denen ja auch so schwer.

Ich möchte Sie bitten, mir diese eine Frage zu beantworten:
Genügt die Menge den Peano-Axiomen?

Die mathematische Fachwelt ist der Überzeugung, daß die CANTORschen Diagonalverfahren richtig sind und ich beweise, daß sie falsch sind. Und jetzt?

Jetzt klären wir das Problem mit den natürlichen Zahlen und dann erkläre ich Ihnen, wo Ihr Gegenbeweis zu Cantor aus dem Ruder läuft.

[Todoroff]

LaughingMan
Sie gehen noch immer davon aus, dass wir über Ihre Beweise diskutieren, aber das stimmt nicht.
Lesen lernen
Es geht einzig und allein darum, dass eine größte natürliche Zahl nicht mit den Peano-Axiomen vereinbar ist.
Glaubensbekenntnis eines Unfähigen.

Und genau hier ist Ihr Problem: Ihre natuerlichen Zahlen, entsprechen nicht den Peano-Axiomen, denn sie widersprechen mindestens einem davon.
Beweisen Sie es!

Und noch einmal: Es gibt keine letzte (ich interpretiere das mal als "größte") Zahl in !
Korrekt

Ich möchte Sie bitten, mir diese eine Frage zu beantworten:
Genügt die Menge den Peano-Axiomen?
Ihre Voraussetzung ist falsch.
...999 ist Teil von N
Ich kenne diesen Unfug (Peano-Axiome) nicht unter diesem Begriff. Welchem soll es denn angeblich nicht genügen?

Jetzt klären wir das Problem mit den natürlichen Zahlen und dann erkläre ich Ihnen, wo Ihr Gegenbeweis zu Cantor aus dem Ruder läuft.
Toll. Und Sie sind sich sicher, sich nicht lächerlich zu machen?
Sie sind unfähig, sich von den Fesseln zu befreien, die Ihnen aufgrund Ihres Studiums angelegt worden sind.
Meine Beweise laufen nicht aus dem Ruder, sondern passen nur nicht in das Schema von Holzköpfen.

Ps 1,4-5
Die Bösen sind wie die Spreu, die der Wind verweht. Drum können die Frevler im Gericht nicht bestehn, noch die Sünder in der Gerechten Gemeinde.

[LaughingMan]

LaughingMan
Es geht einzig und allein darum, dass eine größte natürliche Zahl nicht mit den Peano-Axiomen vereinbar ist.
Glaubensbekenntnis eines Unfähigen.

[...]

Ich kenne diesen Unfug (Peano-Axiome) nicht unter diesem Begriff. Welchem soll es denn angeblich nicht genügen?

Da Sie mein letztes Kompliment an Sie gelöscht haben, möchte ich es gerne wiederholen: Ich mag ihren Humor!

Und genau hier ist Ihr Problem: Ihre natuerlichen Zahlen, entsprechen nicht den Peano-Axiomen, denn sie widersprechen mindestens einem davon.
Beweisen Sie es!

Habe ich wiederholt, aber ich mache es auch nochmal.

Ich möchte Sie bitten, mir diese eine Frage zu beantworten:
Genügt die Menge den Peano-Axiomen?
Ihre Voraussetzung ist falsch.
...999 ist Teil von N

Sie beherrschen einfachste Operationen nicht! Wo behaupte ich in der Frage, dass ...999,0 nicht zu den natürlichen Zahlen gehört? Ich frage ob die Menge, die alle natürlichen Zahlen und ...999,0 enthält den Axiomen genügt.

Wenn ...999,0 schon in enthalten ist, ändert die Vereinigung einfach nichts und man bleibt bei der ursprünglichen Menge. Ist ...999,0 nicht in enthalten, wird sie hinzugefügt und ist so in enthalten.
In beiden Fällen enthält nachher und ...999,0.
Aber mit den Peano-Axiomen würde ich gerne noch etwas warten.



Da das ier eigentlich gar nicht der Thread zu den natürlichen Zahlen ist, habe ich mal in einem passenderen Faden weiter geschrieben.

[LaughingMan]

Weil sich dieser Thread mit 1-0,999... beschäftigt, habe ich auf ihre Bemerkungen zum Thema natürliche Zahlen im dazugehörigen Faden geantwortet (bzw. eigentlich nicht richtig geantwortet, aber das kann man ja da nachlesen).

Hier würde ich gerne nochmal auf die Problematik der unendlichen (weil Nachkommastellen trivialerweise abzählbar sind, ist hier keine explizite Unterscheidung von abzählbar/überabzählbar nötig) Dezimalentwicklung von 0,111... eingehen. Das Gleichnis mit Achilles war durchaus ernst gemeint und ich würde gerne auch Ihre Antwort darauf hören. Die von Herrn Todoroff habe ich bereits und ich würde gerne auf beide antworten.

[Todoroff]

LaughingMan
Aber mit den Peano-Axiomen würde ich gerne noch etwas warten.
Wie IMMER(!) labern Sie nur und kotzen uns Ihre Glaubensbekenntnisse vor die Füße.
Lächerlich, Doktorand der Mathematik. Was man heutzutage alles glauben muß. Es wachsen ganz offensichtlich nur noch Idioten nach.
Diesen Schwachsinn schrieben Sie tatsächlich schon oft, aber es ist eben kein Beweis, nur Gelaber.
Und wieder haben Sie infam gelogen, indem Sie behauptet haben, diesen BEWEIS schon oft erbracht zu haben, obwohl Sie auch diesmal, zum 101. Mal den Beweis nicht erbrachten. Also kommuniziere ich hier mit einem Idioten und mit einem Lügner. Das ändern Sie, oder ich lösche Ihre Beiträge.
Verwirklichen Sie doch EINMAL die Ansprüche selber, die Sie an mich stellen, oder verschwinden Sie einfach.
Ich betrachte Ihre Dummheit (Gegenteil von Weisheit) nicht als Humor.
Wir sind weiterhin nicht über das Stadium Ihrer dämlichen Behauptungen hinausgekommen, und Sie beabsichtigen das auch nicht. Was also wollen Sie? Daß ich alle Ihren Unfug lösche?
Sie sind genauso dämlich wie mein Sohn, der genau Ihr Alter hat. Muß ein FURCHTBARER Jahrgang sein, 1977.

5 Mose 13,4
Der Herr, euer Gott, prüft euch, um zu erkennen, ob ihr das Volk seid, das den Herrn, seinen Gott, mit ganzem Herzen und mit ganzer Seele liebt.

[LaughingMan]

Verwirklichen Sie doch EINMAL die Ansprüche selber, die Sie an mich stellen, oder verschwinden Sie einfach.

Es täte mir Leid, wenn ich irgendwelche mathematikbezogenen Fragen oder vernünftigen Ansprüche an mich nicht beantwortet hätte, bzw. diesen nicht gerecht geworden wäre, aber mir fällt für beides kein Beispiel ein - haben Sie eines? Wenn ich mich nicht irre, waren ihre letzten Fragen:

• Beweis, dass ...999,0 nicht mit den Peano-Axiomen vereinbar ist.
  Antwort hier; in der Nummerierung unter 3.
• Die Frage danach, wie ich argumentieren könnte, ohne ihren "Beweis" verstanden zu haben.
  Antwort hier; oben zwischen den ersten beiden Zitatboxen.
• Die Aufforderung, die letzte Zahl aus zu nennen.
  Antwort in obigem Post weiter unten.
• Die Frage nach dem Personenkreis, der die Gültigkeit von gewissen Axiomen für gewisse Mengen fordert.
  Antwort im selben Post ein Absatz weiter unten.
• Die Frage, welche Menge ich zum Zählen einführen wolle.
  Die Antwort befand sich im gelöschten Post. Kurzform: Gar keine.
• Die Frage nach den (un)echten Zahlen.
  Die Antwort befand sich im gelöschten Post. Kurzform: Es gibt sie nicht - es handelte sich um einen Namensvorschlag.

Weiter zurück zu gehen erscheint mir unnötig. Ihnen sollte spätestens jetzt auffallen, dass ich jede Frage zur Mathematik beantworte* (wenn auch meist nicht in Ihrem Sinne) - ganz im Gegensatz zu Ihnen, der auf diese Widersprüche (besonders 2. und 3.) seit 31 Monaten nicht geantwortet hat, außer mit dem Verweis, dass dies nicht nötig sei.
Umso interessanter ist diese Behauptung ob der Tatsache, dass beide Widersprüche direkt von Ihren Behauptungen abgeleitet sind, auf Ihrer HP aber nicht erwähnt werden und es mir so nicht möglich ist, Ihre Meinung zu vermuten. Ich muss sie erfragen und Sie weigern sich weiterhin zu antworten.

* Zu dem aktuellen Thema gibt es keine offenen Fragen an mich und nur eine an Mileva (das Gleichnis mit Achilles). Sobald ich seine (ihre?) Antwort habe, oder so viel Zeit verstrichen ist, dass ich nicht mehr davon ausgehe, eine zu bekommen, werde ich das auch weiterführen.

[Elrik]

Ergo: Die Ermittlung einer größeren natürlichen Zahl ist unmöglich....999,0 ist also die größte natürliche Zahl, die wir benennen können.

Wenn man die Punkte betrachtet, könnte man davon ausgehen, dass die neunhundertneunundneunzig Punkte die größt mögliche Menge natürlicher Punkte ist, wobei Gott die natürlichen Punkte und auch die natürliche Kommanull schuf, wovon es nur eine einzige gibt und zwar im Garten zwischen Kürbis und Melone nicht weit entfernt von den Wurzeln und Potenzen, kaum zu verfehlen.

[Elrik]

ergibt das dann eine größte denkbare reelle Zahl ...999,999..., die dann größer ist als die größte denkbare natürliche Zahl?

Wenn es ihnen nützt, wird es ihren Nächsten nützen.
Auf Ihre Kosten zu leben nützt mir - Ihnen auch?
Unendlich groß : ">...999", unendlich klein: "0,111...>", anders: "..." wird es nie gewesen sein.

[Elrik]

um das zu wissen reicht ein Abschluss 10. Klasse.

JA, der bereichert alle Menschen, so ein Schriebsel ist echt viel wert, kann man sich den Hintern putzen, ohne seine Hände zu beschmutzen. In Sofern haben Sie vollkommen Recht, allerdings gibt es nach jedem Halbjahr so ein Wisch, ein bischen viel finden sie nicht?

Außerdem ist es keine Problematik.

Sicher keine, die Sie angehen müsste.

Die Menge der Natürlichen Zahlen und deren axiomatische Definition wird bereits in der Schule behandelt.

Das sagt der charismatische Axel Omatisch oder wer?

Und ein Axiom besagt Wobei n' = n+1.

n ist keine Zahl. Aber das braucht Sie nicht zu interessieren, sie brauchen bestimmt auch keine Rechnungen zu bezahlen, denn da werden keine Variablen verwendet, weil nämlich Menschen die Variable sind.

Oder verbal.

Nein, vokabularisch. Die Trickkiste von Illusionisten ist immer kleiner als deren Wortschatz, genannt Vokabular.

Jede natürliche Zahl besitzt einen Nachfolger, ob wir den uns vorstellen können oder nicht. Meinetwegen soll ja ...999.0 die größte "vorstellbare" natürliche Zahl sein, es ist aber nicht die größte und hat für die Mathematik keinerlei Bedeutung.

Von jeder ZAHL ist anzunehmen, dass sie eine Nächste hat. Das ist beim Menschen auch so. Also die Nächste und der Vorfahre der 9 ist 10 und 8, von der 99 sind es 100 und 98, von neunhundertneunundneunzig sind es Tausend und Neunhundertachtundneunzig, ...999,0 ist keine Zahl, hat keinen Nachfolger und keinen Vorfahren, weil unklar ist wie sich die Vorfahren und die nachkommen in den Und-so-weiter-Punkten (u.s.w. = drei Punkte) widergespiegeln. ...999,0 hat jedoch einen Schöpfer, aber auch 999 und 8 und 0 und , .

[Karl-Heinz Prügel]

um das zu wissen reicht ein Abschluss 10. Klasse.

Da Sie sich nicht weiter zu Ihrer Qualifikation äußern, schließe ich daraus, daß Sie Hauptschüler waren, asozial sind und Gras rauchen.

[Todoroff]

Omega
Unendlich ist übrigens keine natürliche zahl.
sagt wer?
Was ist UNENDLICH für eine Zahl, wenn es keine natürliche ist?
Wie kann 1/n Null ergeben, durchläuft n die Menge der natürlichen Zahlen?

Tun Sie mal etwas Ungewöhnliches!
Bezahlen Sie eine Ihrer offenen Rechnungen!