Die (x,t)-Koordinaten sind IMMER(!) die Koordianten von Lichtsignalen, weshalb IMMER gilt: x=ct
weil das Voraussetzung(!) ist.
DAS ist und bleibt eben leider Ihr falscher Glaube. Dass Sie diesem so verhaftet sind, obwohl in Einsteins "Büchlein" ausdrücklich auch Koordinaten fahrender Züge Lorentz-Transformationen unterzogen werden, ist vielleicht durch die Umstände zu erklären, die Sie bei Ihren fruchtlosen Versuchen vor 3 Jahrzehnten, Ihre Gedanken mit "Experten" zu diskutieren, erleben mussten.
Wie also können wir uns trotz allem auf dem Boden der Tatsachen der Angelegenheit nähern? Das kann ich schwer einschätzen. Ich schlage vor, für eine Weile den größeren Zusammenhang, in den die Lorentztransformationen bei Einstein eingebettet sind, die Rolle Einsteins und seiner "Jünger" im Krieg gegen Gott usw. beiseite zu lassen, solange es "nur" um Dinge wie Nullteilung und innere Widersprüche geht, für deren Beurteilung diese Gesichtspunkte nicht unmittelbar relevant sind.
Also: Bewegungen, z.B. von Teilchen, lassen sich beschreiben, indem man in der Umgebung der Teilchen Raumkoordinaten (x,y,z, im Fall eindimensionaler Bewegung nur x) festlegt (mit Hilfe eines "Urmeters"), bestimmte Uhren für "gültig" erklärt (darunter wird man naheliegenderweise wohl erstmal keine Synchronisation mittels Lichtstrahlen verstehen, sondern eher, dass sie am gleichen Ort gleich gestellt werden, dann im Raum verteilt werden und nur so lange benutzt werden, wie erfahrungsgemäß nach erneutem Einsammeln an denselben Ort keine Abweichungen untereinander festzustellen sind) und mit deren Hilfe angibt, welche Raumkoordinaten (x,y,z, z.B. in Metern) zu welchen Zeiten (t, z.B. in Sekunden) durchlaufen werden. Da zu einem Zeitwert immer nur ein Raumpunkt festzustellen ist, kann man dies z.B. angeben, indem man x ( und ggf. y,z) als Funktion von t darstellt: x(t)=2t, y(t)=0, z(t)=0 steht für eine geradlinige unbeschleunigte Bewegung mit Geschwindigkeit 2 m/s in x-Richtung. x(t)=3t, y(t)=4t, z(t)=0 ebenfalls für eine geradlinige unbeschleunigte Bewegung, die zur Zeit 0 den als solchen festgelegten Nullpunkt und zur Zeit 1 den Punkt (3,4,0) durchläuft, in dieser Zeit also eine Distanz von

(Metern) zurücklegt, also eine Geschwindigkeit von 5 m/s hat.
Statt t als freien Parameter zu verwenden und x als Funktion von t anzugeben, könnte man genauso gut t, x, y, z als Funktion von einem anderen, neu einzuführenden Parameter s angeben, die erste Bewegung also z.B. als t(s)=s, x(s)=2s (y(s)=0, z(s)=0), oder auch als t(s)=2s+1, x(s)=4s+2: Durchläuft s alle Werte (reellen Zahlen), so durchlaufen t und x in allen diesen Fällen dieselben Wertepaare. An dieser Stelle sind solche Beschreibungen natürlich nur Verkomplizierungen. s hat i.A. keine Bedeutung analog zu t als "Zeit", sondern dient nur der "Aufzählung".
x als Funktion von t kann man in ein zweidimensionales Koordinatensystem mit t- und x-Achse einzeichnen. Das ist nun mal so und bedeutet nicht zwangsläufig, dass t als identisch mit einer weiteren Raumkoordinate bzw. t und x nur gemeinsam als "Raumzeit" zu betrachten sind. Verwendet man die Beschreibung mit dem Parameter s, dann kann man (t, x) als Funktion von s in ein dreidimensionales Koordinatensystem mit s-, t- und x-Achse "zeichnen". Oder man berechnet nacheinander für verschiedene s den t- und x-Wert, zeichnet diese Wertepaare in ein zweidimensionales (t,x)-System und notiert (z.B. als Zahl) an den Punkten, welcher s-Wert dazugehört. Oder man lässt es bleiben, wenn s unwichtig ist. Im Fall einer dreidimensionalen Bewegung, wenn x,y,z als Funktionen von t (oder t,x,y,z als Funktionen von s) gegeben sind, kann man nichts zeichnen und auch nicht gezeichnet denken, da vier- oder fünfdimensionale Koordinatensysteme nicht vorstellbar sind. Dieses Zeichnen ist aber für die Beschreibung der Bewegung auch nicht notwendig.
So beschreibt man also Bewegungen. Die Koordinaten sind willkürlich, man kann sie ändern, z.B. ein nur halb so langes Urmeter benutzen, dann wird aus jedem bisherigen x-Wert der neue Wert x'=2x, wenn man außerdem auf dreimal so schnelle Uhren umsteigt, wird aus t der neue Wert t'=3t. Gewisse Fragestellungen kann man, wenn Bewegungen in diesen gestrichenen Koordinaten angegeben werden, mit denselben Rechenmethoden beantworten wie in den ungestrichenen Koordinaten, z.B. die Frage, ob ein Körper irgendwann einen anderen überholt, wie oft sie sich begegnen o.ä. Für manche andere Fragestellungen, die konkrete Zahlenwerte betreffen, kann man nicht einfach im gestrichenen System rechnen, als wäre es das ungestrichene, sondern muss zunächst die Transformation rückgängig machen. Jedenfalls ist die genannte Transformation uneingeschränkt wohldefiniert und kann zu keinen mathematischen Widersprüchen führen.
Eine anderer, mathematisch möglicher Koordinatenwechsel wäre eine sogenannte "Lorentztransformation" der Form
})
}\,\,\,,)
wobei c für die Vakuumlichtgeschwindigkeit (in m/s) und w für eine fest vorgegebene, nicht von t oder x abhängige Zahl mit |w|<c steht.
Auch dieser Koordinatenwechsel ist eine wohldefinierte Funktion von t und x, man kann alle t- und x-Werte einsetzen. Innere Widersprüche können nicht auftreten.
Betrachten wir eine Bewegung mit Geschwindigkeit c, in den ungestrichenen Koordinaten beschrieben durch t=s, x=cs. Dass die Geschwindigkeit c ist, stellt man (da die Bewegung geradlinig-gleichförmig ist) fest, indem man zwei s-Werte auswählt, die zugehörigen x-Werte subtrahiert und durch die Differenz der zugehörigen t-Werte teilt. Z.B:

.
Nach Anwenden der Lorentztransformation erhält man
}{\sqr(1-\frac{w^2}{c^2})})
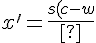}{\sqr(1-\frac{w^2}{c^2})}\,\,\,.)
Zeichnet man diese Werte in ein (t',x')-Koordinatensystem, erhält man wieder eine gerade Linie. Wenn man jetzt zwei s-Werte auswählt und die Differenz der zugehörigen x'-Werte durch die Differenz der t'-Werte teilt, erhält man wieder c. Ob eine gegebene Bewegung bezüglich der ungestrichenen Koordinaten Geschwindigkeit c hat, kann man also anhand der gestrichenen Koordinaten mit derselben Technik feststellen wie anhand der ungestrichenen.
Für andere Geschwindigkeiten ist das nicht der Fall: Wendet man auf t=s, x=ws (Bewegung mit vorgegebener Geschwindigkeit w<c) die Lorentztransformation an - was natürlich genauso gut möglich ist wie bei c statt w -, erhält man
}{\sqr(1-\frac{w^2}{c^2})})

Wendet man auf darauf die "Technik" an, mit der man aus den ungestrichenen Koordinaten die Geschwindigkeit ermitteln würde, erhält man 0.
Soweit (die harmlosen Dinge) erstmal klar? Oder sehen Sie hier schon Fehler?
Lesen Sie doch mal (...)
Längst geschehen - das ist ja überall unübersehbar platziert...